| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 코기토논증
- 참여문제
- 인문적삶
- 본유 관념
- 인식주체
- 동일자문제
- 아리스토텔레스
- 플라톤
- 타인의평가
- 실재론
- 성숙한사회
- 물리주의
- 중세철학
- 방법론적회의
- 시공간연속성
- 합리론 경험론
- 야구물리학
- 충격점
- 개별화원리
- 보편자논쟁
- 악플문화
- 칸트비판
- 확률해석
- 스포츠물리학
- 명석판명
- 평가문화
- 측정문제
- 평가사회
- 질료형상론
- 존재와속성
- Today
- Total
Jacobyechankim
스위트 스팟 Sweet spot의 의미와 원리 : 타격 중심점 Center of percussion과 최대 반발점 Best bounce spot 본문
스위트 스팟 Sweet spot의 의미와 원리 : 타격 중심점 Center of percussion과 최대 반발점 Best bounce spot
jacobyechankim 2024. 5. 16. 00:520. 들어가기
야구와 배드민턴에서 중요한 스윗 스팟의 물리학적 원리를 타격 중심점 Center of percussion과 최대 반발점 Best bounce spot을 통해 깊이 탐구해본다.
1. 이론
1-1. 개요
야구공을 방망이로 휘두를 때 어떨 때는 손이 매우 아프기도 하고 쳤는지도 모를 정도로 아무 느낌이 없을 때도 있다. 같은 운동 에너지를 가지고 방망이를 휘두르는데도 불구하고 이처럼 손잡이에 가해지는 충격이 다른 이유는 야구공이 방망이의 어느 위치에 충돌하는지에 따라 달라지기 때문이다. 구체적으로는, 야구공이 방망이에 충돌했을 때 방망이의 위치에 따른 각 부분마다 각기 다른 힘을 받아 새로운 운동을 하게 되는데, 이때 받는 힘이 0인 지점도 있고 큰 지점도 있다는 것이다. 이번 실험에서 알아볼 두가지 중 하나인 Center of percussion(COP)이 바로 그 힘이 0인 지점이다. 다른 하나는 Best bounce spot(BBS)으로 불리는 지점으로, 야구공을 홈런치듯 가장 세게 쳐낼 수 있는 충격점의 위치를 알아볼 것이다. COP와 BBS의 위치를 이론을 통해 유도해본다.
1-2. COP
야구공이 방망이와 충돌할 때 방망이에게 일어나는 사건을 분석하기 전에 분석의 편의를 위해 몇 가지를 짚어보자면 다음과 같다. 방망이를 휘두를 때 야구공과 충돌하는 충돌시점 직전의 방망이의 운동 상태는 충돌 후 변화하게 된다. COP를 특정짓기 위해서는 변화하는 양만을 보면 되므로, 공중에 자유롭게 놓여 정지해 있는 방망이에 대해 야구공이 충돌하는 상황을 살펴보아도 동일할 것이다.
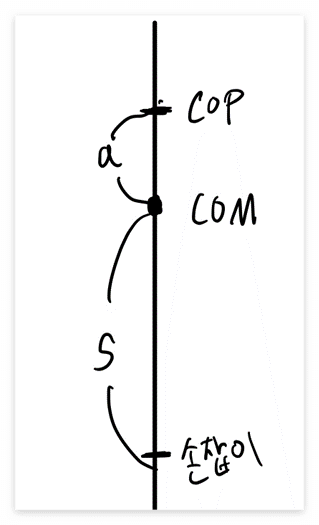
야구공이 방망이의 어느 지점에 충격을 가하면 방망이는 병진운동과 회전운동을 병행한다. 병진운동에 의해 생긴 각 지점의 선속도는 동일할 것이고, 마찬가지로 회전운동의 각속도는 서로 동일할 것이다. 즉, 강체(Rigid)에 대한 분석을 하는 것인데, 강체의 병진운동은 마치 무게중심에 위치한 같은 질량의 입자에 힘을 가하는 것과 동일하다. 강체의 회전운동은 무게중심을 회전축으로 한 회전운동과 동일하다.
먼저, 위의 이론을 바탕으로 COP의 위치를 직관적으로 잡아보도록 한다. COM의 밑쪽에 손잡이를 두었을 때, COM 밑쪽에서 야구공이 충돌해 충격력이 오른쪽 방향으로 작용했다고 가정해보자. 손잡이 부분에서는 오른쪽 진행 방향의 병진운동과 COM을 중심으로 시계 반대 방향의 회전운동의 벡터합으로 운동하게 될 것이다. 즉 손잡이에 힘이 작용한다는 것이므로 COP는 COM 아래쪽에 위치하지 않는다는 것을 알 수 있다. 반대로 COM 윗쪽에 충격력이 가해지면 손잡이 부분의 병진운동은 오른쪽으로, 회전운동은 시계방향으로 진행되기 때문에 손잡이에 작용하는 힘이 아마 0이 될 수 있을지도 모른다. 정리하자면, COP와 손잡이는 COM을 중심으로 서로 반대쪽에 위치해야 한다. Fig.1은 이를 나타낸 모식도이다.
Fig.1의 상황에서 COM 윗쪽에 a만큼 떨어진 곳에 충격력이 작용했을 때, 방망이에 대한 병진운동과 회전운동을 서술하는 다음의 (1), (2)가 성립한다.
$$\begin{equation} F=Ma' \end{equation} $$
$$\begin{equation} Fa=I_{CM}\alpha \end{equation} $$
여기서 $F$는 야구공이 가하는 힘, $M$은 방망이의 질량, $a'$은 병진운동 가속도, $I_{CM}$은 무게중심에 대한 관성모멘트, $\alpha$는 각가속도이다. 만약 COM으로부터 $a$만큼 떨어진 위치에 야구공이 충돌했을 때 정말 손잡이에 아무런 운동상태 변화를 주지 못한다면 그 충격 지점이 바로 우리가 찾던 COP가 될 것이다. 따라서 손잡이의 선가속도가 0이 되도록 하는 $a$를 찾아주면 된다.
$$ a_{손잡이}=a-s\alpha=0 $$
$$ F(\frac{1}{M}-\frac{as}{I_{CM}})=0 $$
$$ \begin{equation} \therefore a=\frac{I_{CM}}{sM} \end{equation} $$
(3)을 구체적으로 이해해보자면, $a$와 $s$는 서로 대칭적인 변수임을 알 수 있고 따라서 손잡이를 $s$위치에, 충격지점을 $a$위치에 설정해도 마찬가지로 손잡이의 가속도가 0이 되는 COP가 된다.
1-3. BBS
개요에서 설명한 바와 같이, 특정 회전운동 에너지를 가진 방망이가 야구공에 전달하는 운동 에너지의 양은 충격지점의 위치에 따라 달라질 것이다.

충격 직전의 방망이의 각속도를 $w_1$, 충돌 후를 $w_2$라고 하고, 방망이의 관성모멘트를 $I$라고 하자. 완전 탄성 충돌로 가정했을 때, 충돌 시점 직전과 직후에 대해 역학적 에너지 보존법칙과 각운동량 보존 법칙을 적용할 수 있다. ($l$을 $I$와 혼동하지 않기 위해 $L$로 표기한다.)
$$ \begin{equation} Iw_1^2=Iw_2^2+mv^2 \end{equation}$$
$$ \begin{equation} Iw_1 = -Iw_2+Lmv \end{equation}$$
$w_1$은 막대의 질량중심의 위치에너지가 모두 회전운동 에너지로 변화한 것이므로, 막대의 초기 고정 각도를 알면 쉽게 구할 수 있다. (4)와 (5)에서 $w_2$를 소거해 $v$를 구하면 다음과 같다.
$$I(w_1+w_2)(w_1-w_2)=mv^2$$
$$Lmv(w_1-w_2)=mv^2$$
$$\begin{equation} w_2=w_1-\frac{mv^2}{Lmv} \end{equation}$$
(6)을 (5)에 대입해 $v$로 정리하면,
$$\begin{equation} v=\frac{2LIw_1}{I+L^2m} \end{equation}$$
따라서 $v(L)$의 개형은 Fig.3처럼 주어진다.
(7)에서 $I, w_1, m$은 $L$과 독립변수인 constant이다. 따라서 운동 에너지 $E_k=\frac{1}{2}mv^2$에서 m은 L과 독립변수이므로 $E_k(L)$은 $v(L)$이 최대일 때 최댓값을 갖는다. $v'(L)=0$의 해를 구해 BBS의 위치를 계산하면 다음과 같다.
$$\begin{equation} (BBS)=\sqrt{\frac{I}{m}} \end{equation} $$
야구공의 질량에 따라 BBS의 위치가 달라진다는 점은 뭔가 신기하다.

2. COP와 단진자
COP의 위치를 구할 수 있는 다른 실험적 방법으로 단진자를 이용하는 방법이 있다. COP의 위치를 서술하는 (3)에 대해 복합진자의 운동을 생각해볼 수 있는데, 방망이의 손잡이를 회전점으로 진자운동을 시키면 얻게 되는 주기는 다음과 같다.
$$T=2\pi \sqrt{ \frac{I_{CM}+s^2M}{Mgs} }=2\pi \sqrt{ \frac{a+s}{g} }$$
한편, 이 주기는 길이가 $a+s$인 단진자의 주기와 동일하다. 따라서 방망이를 진자운동 시켜놓고, 단진자의 길이를 변경하며 서로 같은 주기가 되는 길이를 찾으면, 회전점으로부터의 COP의 위치인 $a+s$를 실험적으로 구할 수 있다. 물론, 운동 반경이 작아야 한다.
3. 여담
BBS와 COP는 야구와 배드민턴 같은 스포츠를 할 때 유용하게 쓰일 수 있는 전략이다. 실제로 야구방망이와 배드민턴 채를 설계할 때에도 이 두 SPOT을 고려해 제작하며, 선수들은 손잡이의 위치와 이에 대응되는 SPOT을 손에 익히기 위해 훈련한다.
야구방망이로 야구공을 칠 때 충격점을 잘못 잡아 치게 되면 손에 큰 무리가 오는 경험을 할 수 있는데, 이는 COP 설명 부분에서 설명한 바와 같이 회전점에 적용되는 충격력 때문이기도 하고, 한 가지 더로는 방망이의 진동이 울리는 것도 영향을 준다. 방망이의 진동 주파수는 타점에 따라 달라지므로 이를 고려해 방망이를 휘둘러 야구공을 맞출 때 잘 맞춰야 한다.
한편 COP와 BBS 외에 다른 성질을 가진 지점들도 존재하는데, 테니스 라켓에서는 맨 윗부분부터 순서대로 Dead spot, node, COP, BBS, CM이 위치한다고 알려져 있다. Dead spot은 공이 라켓에 맞았을 때 공의 운동 에너지가 라켓에 전부 전달돼, 공의 속력이 0이 되는 지점이다. Node는 공과 충돌한 라켓의 진동의 진폭이 0이 되는 지점으로 sweet spot으로 불리기도 한다. 이처럼 지점별로 테니스 라켓을 휘둘러 공을 치는 과정을 분석할 때 물리학적으로는 이중 진자 모델로 해석한다고 한다.
4. 참고 문헌
1. physics usyd edu, physics of baseball & softball, http://www.physics.usyd.edu.au/~cross/baseball.html
The physics of baseball
www.physics.usyd.edu.au
2. physics usyd edu, physics of tennis, http://www.physics.usyd.edu.au/~cross/tennis.html
Tennis Raquet Physics
PHYSICS OF TENNIS The behaviour of racquets and balls is governed mainly by Newton’s three Laws of Tennis. These laws are fully explained in our book The Physics and Technology of Tennis. The following is a summary of a few topics of interest to give you
www.physics.usyd.edu.au
3. physics Forums, What Is the Physics Behind the Sweet Spot on a Baseball Bat?, https://www.physicsforums.com/threads/what-is-the-physics-behind-the-sweet-spot-on-a-baseball-bat.1000989/
What Is the Physics Behind the Sweet Spot on a Baseball Bat?
Hitting a baseball in the sweet spot on a baseball bat gives the best rebound and does not twist the handle of the bat in the hitter's hand. How is this spot and its behavior described in Mechanics? A similar question: The bumper on a pool table is at a he
www.physicsforums.com
4. 동아사이언스, 물리학으로 본 정현의 ‘테니스 신드롬’, http://m.dongascience.com/news.php?idx=21654
물리학으로 본 정현의 '테니스 신드롬'
'테니스 신드롬'을 불러 일으킨 정현(22·한국체대). 정현이 세운 기록의 비결을 과학자가 분석했다. “조코비치보다 젊기 때문에 체력에서 유리했다.” 1월 말 호주 멜버른에서 열린 2018 호주오
m.dongascience.com
